Các Đại Lượng Thống Kê Mô Tả: Hướng Dẫn Chi Tiết & Dễ Hiểu

December 25, 2024

Các Đại Lượng Thống Kê Mô Tả: Hướng Dẫn Chi Tiết & Dễ Hiểu

Trong phân tích dữ liệu, việc nắm vững các đại lượng thống kê mô tả là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết về các đại lượng thống kê này, giúp bạn tóm tắt và mô tả dữ liệu một cách hiệu quả. Bạn có bao giờ cảm thấy bối rối trước một tập hợp dữ liệu, không biết bắt đầu từ đâu? Làm thế nào để biến những con số khô khan thành thông tin có ý nghĩa? Đó chính là lúc bạn cần đến sự trợ giúp của các đại lượng thống kê mô tả.

Thống Kê Mô Tả Là Gì?

Trước khi đi sâu vào chi tiết về các đại lượng thống kê mô tả, chúng ta hãy cùng nhau nhắc lại một chút về khái niệm thống kê mô tả. Thống kê mô tả (descriptive statistics) là một nhánh của thống kê học, tập trung vào việc tóm tắt, mô tả và trình bày các đặc điểm chính của một tập dữ liệu. Mục tiêu chính của thống kê mô tả là giúp chúng ta hiểu rõ hơn về dữ liệu mà chúng ta đang có, thông qua việc sử dụng các số liệu thống kê, bảng biểu và đồ thị.

Khác với thống kê suy diễn (inferential statistics), vốn sử dụng dữ liệu mẫu để đưa ra kết luận về một tổng thể lớn hơn, thống kê mô tả chỉ tập trung vào việc mô tả các đặc trưng của chính dữ liệu đó.

Các bước cơ bản trong quá trình thống kê mô tả bao gồm:

Thu thập dữ liệu.
Phân loại dữ liệu.
Tính toán các phép đo thống kê.
Trình bày dữ liệu bằng bảng biểu và đồ thị.
Diễn giải kết quả.

Hiểu rõ về thống kê mô tả là nền tảng quan trọng để bạn có thể phân tích dữ liệu cơ bản một cách hiệu quả. Tìm hiểu thêm trên Mạng tài liệu SPSS trên dribbble

Đại Lượng Thống Kê Là Gì?

Vậy, cụ thể thì đại lượng thống kê là gì? Đại lượng thống kê (statistical measure) là một giá trị đặc trưng, được tính toán từ dữ liệu mẫu hoặc dữ liệu tổng thể, dùng để tóm tắt hoặc mô tả một khía cạnh nào đó của dữ liệu. Nói một cách đơn giản, đại lượng thống kê giúp chúng ta rút ra những thông tin quan trọng từ dữ liệu phức tạp.

Các đại lượng thống kê mô tả có mục đích chính là:

Tóm tắt dữ liệu: Sử dụng các giá trị đặc trưng để biểu diễn cho toàn bộ tập dữ liệu.
Mô tả dữ liệu: Sử dụng các phép đo để làm nổi bật các đặc điểm của dữ liệu (ví dụ: vị trí trung tâm, độ phân tán).
So sánh dữ liệu: Cho phép so sánh các đặc điểm của các tập dữ liệu khác nhau.

Các đại lượng thống kê mô tả có thể được chia thành ba nhóm chính:

Các đại lượng đo lường trung tâm: Mô tả vị trí trung tâm của dữ liệu.
Các đại lượng đo lường độ phân tán: Mô tả mức độ phân tán của dữ liệu xung quanh giá trị trung tâm.
Các đại lượng đo lường vị trí: Mô tả vị trí tương đối của một điểm dữ liệu trong tập dữ liệu.

Việc nắm vững khái niệm đại lượng thống kê giúp chúng ta hiểu rõ hơn về ý nghĩa của các phép đo trong thống kê mô tả.

Bạn đang bối rối với việc phân tích dữ liệu SPSS và tìm kiếm một giải pháp đáng tin cậy? Hãy liên hệ dịch vụ xử lý số liệu SPSS chuyên nghiệp, từ xử lý dữ liệu thô đến phân tích sâu và diễn giải kết quả. Cam kết đáp ứng mọi yêu cầu, từ cơ bản đến phức tạp, với quy trình minh bạch, chi phí cạnh tranh, và chất lượng vượt trội.

Các Đại Lượng Đo Lường Trung Tâm

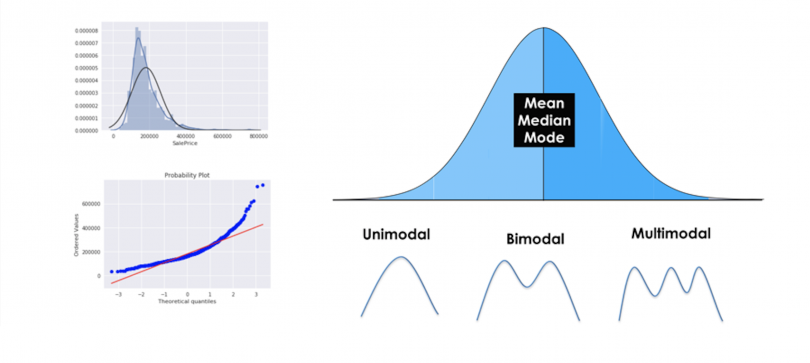
Các đại lượng thống kê mô tả đo lường trung tâm giúp chúng ta xác định vị trí trung tâm của dữ liệu. Chúng ta sẽ cùng nhau tìm hiểu chi tiết về mean, median và mode.

Mean (Trung bình):

Định nghĩa: Giá trị trung bình của tập dữ liệu, được tính bằng cách cộng tất cả các giá trị rồi chia cho số lượng giá trị.
Cách tính: (x1 + x2 + x3 + ... + xn) / n, trong đó n là số lượng giá trị.
Ưu điểm: Dễ tính toán, dễ hiểu.
Nhược điểm: Bị ảnh hưởng bởi các giá trị ngoại lai (outliers).
Sử dụng khi: Dữ liệu có phân phối tương đối đối xứng và không có giá trị ngoại lai.

Median (Trung vị):

Định nghĩa: Giá trị nằm ở giữa tập dữ liệu khi dữ liệu được sắp xếp theo thứ tự.
Cách xác định: Sắp xếp dữ liệu theo thứ tự tăng dần, nếu số lượng giá trị là số lẻ thì median là giá trị chính giữa, nếu số lượng giá trị là số chẵn thì median là trung bình cộng của hai giá trị chính giữa.
Ưu điểm: Không bị ảnh hưởng bởi các giá trị ngoại lai.
Nhược điểm: Khó tính toán hơn mean.
Sử dụng khi: Dữ liệu có phân phối lệch hoặc có giá trị ngoại lai.

Mode (Mốt):

Định nghĩa: Giá trị xuất hiện nhiều lần nhất trong tập dữ liệu.
Cách xác định: Đếm số lần xuất hiện của mỗi giá trị, giá trị nào xuất hiện nhiều nhất là mode.
Ưu điểm: Dễ xác định, đặc biệt hữu ích với biến định tính.
Nhược điểm: Có thể có nhiều mode hoặc không có mode.
Sử dụng khi: Quan tâm đến giá trị phổ biến nhất trong dữ liệu.

Việc lựa chọn sử dụng mean, median hay mode phụ thuộc vào đặc điểm của dữ liệu và mục đích phân tích của bạn.

Mean (Trung Bình)

Để hiểu sâu hơn về đại lượng mean, chúng ta sẽ đi vào chi tiết về định nghĩa, ưu nhược điểm và cách sử dụng của nó.

Định nghĩa: Như đã nói ở trên, mean (trung bình) là giá trị trung tâm của tập dữ liệu, được tính bằng cách cộng tất cả các giá trị rồi chia cho số lượng giá trị. Công thức tính mean thường được ký hiệu bằng chữ x có gạch ngang trên đầu (x̄).
x̄ = (x1 + x2 + x3 + ... + xn) / n
Trong đó:
* x̄ là trung bình mẫu.
* x1, x2, ..., xn là các giá trị trong tập dữ liệu.
* n là số lượng giá trị.

Ưu điểm của mean:

Dễ tính toán: Mean là một phép tính đơn giản, dễ thực hiện.
Dễ hiểu: Kết quả mean dễ dàng được diễn giải và hiểu được ý nghĩa của nó.
Sử dụng tất cả các giá trị: Mean sử dụng tất cả các giá trị trong tập dữ liệu, do đó nó phản ánh toàn bộ thông tin trong dữ liệu.

Nhược điểm của mean:

Bị ảnh hưởng bởi các giá trị ngoại lai: Khi có các giá trị quá lớn hoặc quá nhỏ (outliers), mean sẽ bị kéo lệch về phía các giá trị này, dẫn đến kết quả không phản ánh chính xác vị trí trung tâm của dữ liệu.

Trường hợp nên sử dụng mean:

Dữ liệu có phân phối tương đối đối xứng: Khi các giá trị trong tập dữ liệu phân bố đều quanh giá trị trung tâm, mean là một đại lượng thích hợp để mô tả vị trí trung tâm.
Dữ liệu không có giá trị ngoại lai: Khi dữ liệu không có các giá trị quá lớn hoặc quá nhỏ, mean sẽ phản ánh chính xác vị trí trung tâm.

Ví dụ minh họa:

Nếu bạn có dữ liệu về chiều cao của 5 người: 160cm, 165cm, 170cm, 175cm, 180cm, thì chiều cao trung bình (mean) sẽ là: (160+165+170+175+180)/5 = 170cm.

Tìm hiểu thêm các kênh tại các đơn vị Hỗ trợ SPSS trọn gói

Median (Trung Vị)

Tiếp theo, chúng ta sẽ cùng nhau tìm hiểu về đại lượng median (trung vị).

Định nghĩa: Median (trung vị) là giá trị nằm ở vị trí chính giữa của tập dữ liệu khi dữ liệu được sắp xếp theo thứ tự từ nhỏ đến lớn.

Cách xác định:

Sắp xếp dữ liệu theo thứ tự tăng dần.
Nếu số lượng giá trị (n) là số lẻ, median là giá trị ở vị trí (n+1)/2.
Nếu số lượng giá trị (n) là số chẵn, median là trung bình cộng của hai giá trị ở vị trí n/2 và (n/2) + 1.

Ưu điểm của median:

Không bị ảnh hưởng bởi các giá trị ngoại lai: Median là một đại lượng mạnh mẽ, không bị tác động bởi các giá trị quá lớn hoặc quá nhỏ.
Phù hợp với dữ liệu có phân phối lệch: Khi dữ liệu có phân phối không đối xứng (skewed), median sẽ phản ánh vị trí trung tâm tốt hơn mean.

Nhược điểm của median:

Khó tính toán hơn mean: Để tính median, chúng ta cần sắp xếp dữ liệu theo thứ tự, điều này có thể mất thời gian hơn so với tính mean.
Không sử dụng tất cả các giá trị: Median chỉ sử dụng giá trị ở giữa hoặc hai giá trị ở giữa, bỏ qua các giá trị khác trong tập dữ liệu.

Trường hợp nên sử dụng median:

Dữ liệu có phân phối lệch: Khi dữ liệu có phân phối không đều (ví dụ: có nhiều giá trị nhỏ và một vài giá trị rất lớn), median sẽ cho chúng ta thông tin chính xác hơn về vị trí trung tâm so với mean.
Dữ liệu có giá trị ngoại lai: Khi có các giá trị quá lớn hoặc quá nhỏ trong dữ liệu, median sẽ ít bị ảnh hưởng hơn so với mean.

Ví dụ minh họa:

Nếu bạn có dữ liệu về thu nhập hàng tháng của 7 người (đơn vị: triệu đồng): 3, 4, 5, 6, 7, 10, 50 thì median sẽ là 6. (50 là giá trị ngoại lai, nếu dùng mean thì kết quả sẽ cao hơn nhiều).

Chúng ta đã cùng nhau tìm hiểu về hai đại lượng thống kê mô tả quan trọng là mean và median. Để tiếp tục khám phá về đại lượng mode và các đại lượng khác, mời bạn đón đọc phần tiếp theo của bài viết. Bạn cũng có thể xem thêm các kiến thức về thông kê SPSS trên website luanvanviet.com để hiểu sâu hơn nhé.